Konstruktor - Słup żelbetowy + DXF
Moduł Słup żelbetowy należy do grupy programów wspomagających projektowanie i obliczenia konstrukcji żelbetowych. Program umożliwia analizę statyczną, wymiarowanie i sprawdzanie nośności słupów żelbetowych o dowolnym kształcie przekroju, dwukierunkowo mimośrodowo ściskanych. Wymiarowanie wykonywane jest wg normy: PN-B-03264: 2002. Sprawdzanie nośności słupów w dwukierunkowym stanie obciążenia z wykorzystaniem dokładnej metody normowej i uwzględnieniem wpływu smukłości. Moduł umożliwia wyznaczanie długości wyboczeniowej wg PN-B-03264: 2002. Możliwość dowolnego definiowania schematu podparcia i dowolnego obciążenia słupa. Program wymiaruje elementy słupowe policzone w module Rama 2D.
Program Konstruktor – Słup żelbetowy można rozszerzyć o opcję automatycznego rysunku wykonawczego (w formacie DXF) przez zakup odpowiedniego modułu Rysunki DXF. Pozwala on na automatyczne wykonanie na podstawie obliczeń statycznych i wymiarowania, pełnego rysunku konstrukcyjnego słupów żelbetowych o przekroju prostokątnym. Program wykonuje rysunki słupów pośredniej lub ostatniej kondygnacji z uwzględnieniem występowania rygli jedno lub dwustronnych oraz zmniejszonej szerokości słupa wyższej kondygnacji. Rysunek zawiera: dwa widoki zbrojenia, charakterystyczny przekrój słupa, „wyrzucone zbrojenie” , wykaz stali zbrojeniowej oraz wszystkie niezbędne opisy i wymiarowania.
Podstawowe możliwości programu to, m. in.:
- Sprawdzanie nośności i wymiarowanie słupów w jedno i dwukierunkowym stanie obciążenia.
- Wyznaczanie długości wyboczeniowych poszczególnych prętów konstrukcji z uwzględnieniem ich powiązania z sąsiednimi prętami konstrukcji.
- Uwzględnianie wpływu smukłości.
- Definiowanie dowolnych typów podparcia słupa.
- Definiowanie dowolnych typów obciążeń.
- Tworzenie kombinatoryki obciążeń.
- Możliwość wykonywania obliczeń (sprawdzania nośności lub wymiarowania) w przekroju lub analizując statykę całego elementu.
- Możliwość zadawania zbrojenia jako pola przekroju przy każdej krawędzi lub jako określonej liczby prętów o założonym położeniu i średnicy.
- Rozmieszczenie prętów, w przypadku słupów okrągłych i rurowych (w opcji sprawdzania nośności), automatyczne dla określonej liczby prętów na obwodzie, bądź poprzez podanie współrzędnych w układzie kartezjańskim lub biegunowym.
- Praktycznie nieograniczona dowolność w definiowaniu przekrojów poprzecznych słupa: prostokątne, teowe, dwuteowe, zetowe, kątowe, okrągłe, rurowe.
- Trójwymiarowa wizualizacja danych geometrycznych.
- Wykonywanie obwiedni nośności w dwóch prostopadłych kierunkach.
Funkcjonalność programu w zakresie obliczeń i wymiarowania:
Program wykonuje obliczenia sprawdzania nośności w stanie dwukierunkowego obciążenia dla przekrojów żelbetowych prostokątnych, teowych, dwuteowych, zetowych, kątowych, ceowych, kołowych oraz rurowych. W trybie wymiarowania, w stanie jednokierunkowego ściskania ze zginaniem możliwe jest przeprowadzenie obliczeń dla przekrojów prostokątnych, teowych, dwuteowych, zetowych, kątowych oraz ceowych, zaś w stanie dwukierunkowego mimośrodowego ściskania ze zginaniem dla przekrojów prostokątnych. Program uwzględnia wpływ smukłości słupa poprzez zwiększenie działających momentów obliczeniowych.
Obciążenia
Podczas definiowania obciążeń możliwe jest wybranie typu obciążeń w przekroju lub analizując statykę całego elementu. Wybranie drugiej z tych opcji pozwala na definiowanie dowolnych typów obciążeń. W zakresie warunków podparcia możliwe jest definiowanie dowolnych typów podparcia słupa, niezależnie w dwóch prostopadłych płaszczyznach.
Zbrojenie
Zbrojenie zadawane jest jako pola przekroju wkładek rozmieszczonych przy każdej krawędzi lub jako określona liczba prętów o założonym położeniu w przekroju i średnicy. W przypadku słupów okrągłych i rurowych rozmieszczenie prętów (w opcji sprawdzania nośności) następuje automatycznie (dla określonej liczby prętów na obwodzie), bądź poprzez podanie współrzędnych w układzie kartezjańskim lub biegunowym. Sprawdzanie nośności w stanie dwukierunkowego obciążenia może odbywać się dla następujących przekrojów słupów: prostokątne, teowe, dwuteowe, zetowe, kątowe, okrągłe, rurowe. Wymiarowanie, czyli automatyczny dobór zbrojenia w czterech charakterystycznych punktach słupa (podpora dolna, podpora górna, maksymalny moment w płaszczyźnie xy, maksymalny moment w płaszczyźnie yz) odbywa się: dla dwukierunkowego stanu obciążenia – dla przekroju prostokątnego
Układ współrzędnych
W programie założono dwa układy współrzędnych: globalny (w przypadku definiowania parametrów globalnych dla całego elementu) oraz lokalny (w przypadku definiowania parametrów przekroju). Podczas wprowadzania danych są umieszczane odpowiednie rysunki przedstawiające kierunki założonych osi. zadawanie danych zgodnie z lokalnym układem współrzędnych zostało zastosowane tylko w przypadku definiowania istniejącego zbrojenia w przekroju (sprawdzanie nośności) w celu ułatwienia wprowadzenia położenia prętów.
Przyjęte założenia dla obliczeń.
Założono, że podstawą analizy nośności słupa obciążonego ukośnie mimośrodowo będą obliczenia przeprowadzane niezależnie w dwóch prostopadłych kierunkach X i Y. Wykorzystano założenia norm PN-B-03264:1999 [1] i Eurokod2 [2] dotyczące charakterystyk materiałowych i granicznych stanów odkształcenia. Współczynnik (, uwzględniający dwukierunkowość obciążenia pozostawiono w algorytmie jako wielkość zmienną, której wartość ustala użytkownik programu. Po stronie bezpiecznej jest przyjmowanie a=1 (jest to zgodne z NS 3473 E:1992).
Założenia materiałowe
Naprężenia w betonie ściskanym wg PN-B-03264:2002 określone są wykresem
paraboliczno – prostokątnym (rys. 1), linią ciągłą zaznaczono na rysunku wykres
obliczeniowy, a przerywaną wykres ideowy. Współczynnik acc, uwzględniający wpływ
obciążenia długotrwałego na wytrzymałość betonu i niekorzystny wpływ sposobu
przyłożenia obciążenia, przyjęto wg punktu 2.1.2 normy.
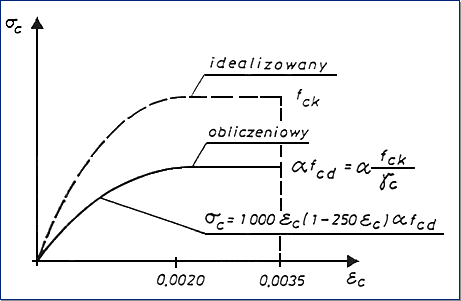
Rysunek1 – Paraboliczno-prostokątny wykres s - e betonu
Wykres dotyczy obciążenia doraźnego, natomiast w obliczaniu słupów, ustalając wpływ smukłości, uwzględnia się pełzanie betonu. Końcowy współczynnik pełzania betonu  przyjmuje się do celów projektowych zgodnie z załącznikiem A normy PN-B-03264:2002 wg tabeli A.1. Podczas ustalania współczynnika pełzania zakłada się, iż naprężenia sc
<0.45fcm(t0) przyjmuje się do celów projektowych zgodnie z załącznikiem A normy PN-B-03264:2002 wg tabeli A.1. Podczas ustalania współczynnika pełzania zakłada się, iż naprężenia sc
<0.45fcm(t0)
Przyjęto dwie wersje zależności ss- es. W przypadku, gdy istnieją
odpowiednie dane doświadczalne dotyczące euk– wartości charakterystycznego
odkształcenia stali odpowiadającego maksymalnej sile, do obliczeń przyjąć można
wykres ss - es z nachyloną gałęzią górną, jak
na rys. 2. W przeciwnym wypadku zakłada się zależność uproszczoną ze stałą
wartością s = fyd dla e P;
fyd/Es.
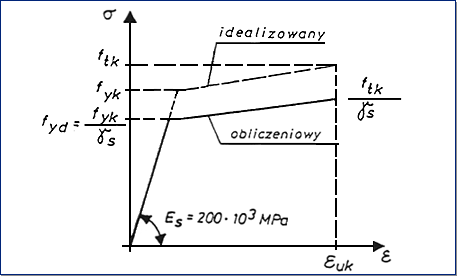
Rysunek2 – Wykress -
e stali zbrojeniowej
Moduł sprężystości stali Es przyjęto zgodnie z pkt. 3.1.3 normy
PN-B-03264:1999 dla przedziału temperatury od -30° C do 200 °C w wysokości:Es = 200 × 103
MPa.
Obliczenia
Założenia do obliczeń przyjęto zgodnie z pkt. 5.1.1 normy PN-B-03264:2002.
Do obliczeń nośności przekroju zginanego w dowolnej płaszczyźnie przyjmuje się za wysokość przekroju h rzut na kierunek prostopadły do osi obojętnej odcinka łączącego najbardziej ściskany lub najmniej rozciągany punkt przekroju z punktem najbardziej rozciąganym lub najmniej ściskanym. Wysokość użyteczną d określa się odpowiednio jako rzut odcinka łączącego punkt najbardziej ściskany lub najmniej rozciągany przekroju z najbardziej rozciąganym lub najmniej ściskanym prętem zbrojenia.
Długości wyboczeniowe
Przyjęto dwa sposoby określania długości obliczeniowych. Pierwszy polega na
bezpośrednim zadaniu tych wielkości przez użytkownika, drugi - na skorzystaniu z metody podanej w załączniku C normy PN-B-03264:2002.
Długości obliczeniowe l0 słupów występujących w żelbetowych
układach ramowych obliczane są wówczas według wzoru: lo=ß
lcol
Wartość współczynnika ß oblicza się na podstawie wzorów podanych w tablicy 1
normy PN-B-03264:2002.
Uwzględnianie wpływu smukłości
Nośność elementów ściskanych sprawdzana jest z uwzględnieniem ich smukłości i wpływu obciążeń długotrwałych, jeżeli zachodzi warunek: lo/h>7 lub
lo/i>25.
Nośność przekrojów przypodporowych występujących w układach o węzłach
nieprzesuwnych sprawdzana jest bez uwzględniania wpływu smukłości.
Wpływ smukłości na nośność elementów żelbetowych uwzględniany jest zgodnie
zpkt. 5.3.2 normy PN-B-03264:2002 przez zwiększenie mimośrodu początkowego
e0 do wartości etot wyznaczanej ze wzoru: etot=
he0
Sprawdzanie nośności
Rozpatrywany przekrój został podzielony na wysokości na skończoną liczbę
warstw. Zbrojenie jest traktowane jako odrębna warstwa o znanym położeniu i
znanym polu przekroju. Sprawdzanie nośności sprowadza się do zbadania, czy siły wewnętrzne w przekroju, policzone z uwzględnieniem wpływu mimośrodu niezamierzonego i smukłości słupa, umieszczone na wykresie (MZ;N) i ewentualnie, w przypadku dwukierunkowego mimośrodowego ściskania, (Mx; N) oraz 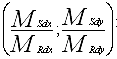 znajdują się wewnątrz obwiedni nośności przekroju. znajdują się wewnątrz obwiedni nośności przekroju.
Tok obliczeń jest następujący:
- przyjęcie jako danego odkształcenia w jednym z włókien przekroju
betonowego, tak by osiągnięty był jeden ze stanów granicznych odkształcenia:
- eS = - 0,0100 w zbrojeniu rozciąganym, lub
eC = 0,0035 w skrajnym ściskanym włóknie betonu, lub
eC= 0,0020 we włóknie betonu odległym o 3/7 h od krawędzi
bardziej ściskanej, zaś ściskana była “góra” przekroju;
- założenie krzywizny przekroju i określenie odkształceń poszczególnych warstw przekroju;
- obliczenie siły normalnej Nc i momentu zginającego
Mc siły w betonie względem początku układu współrzędnych jako sumy
sił normalnych i momentów zginających w poszczególnych warstwach;
- obliczenie sił w zbrojeniu Ns i momentów zginających tych sił
względem początku układu współrzędnych;
- wyznaczenie NRd i MRd jako sumy odpowiednio sił i momentów tych sił w betonie i zbrojeniu;
- powrót do punktu 2 i zmiana krzywizny przekroju, lub, jeśli sprawdzono
cały zakres krzywizny dla założonego odkształcenia, powrót do punktu 1 i
zmiana tego odkształcenia;
- sprawdzenie, czy, dla tego stanu odkształcenia przekroju słupa, dla
którego wartość
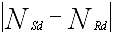
osiąga minimum, spełniony jest warunek:
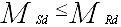 ;
(w.1) ;
(w.1)
- powtórzenie kroków 1 ¸ 7 dla
ściskanego “dołu” przekroju; warunek (1) przyjmuje wtedy postać:
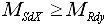 ;
(w.2) ;
(w.2)
w przypadku dwukierunkowego, mimośrodowego ściskania powtórzenie kroków 1
¸ 8 dla drugiego kierunku oraz
sprawdzenie warunku:
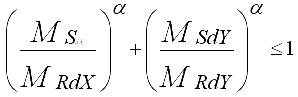 (w.3) (w.3)
Niespełnienie warunku (w.1) lub (w.2) oznacza, że nośność przekroju jest
niewystarczająca ze względu na jednokierunkowe, zaś warunku (w.3) na
dwukierunkowe mimośrodowe ściskanie.
Wymiarowanie
Zakłada się, że szukane zbrojenie rozmieszczone jest w postaci wkładek w
pobliżu przeciwległych krawędzi przekroju. W celu jego obliczenia stosowany jest poniższy algorytm, przy czym wymiarując przekrój ukośnie mimośrodowo ściskany zbrojenie oblicza się osobno dla obu głównych kierunków, przy założonych dwukrotnie większych niż w rzeczywistości momentach zginających.
Tok obliczeń jest następujący:
- przyjęcie jako danego odkształcenia skrajnego ściskanego włókna przekroju
z przedziału De do 0,0035, gdzie
De oznacza przyjęty skok
odkształcenia;
- założenie krzywizny przekroju i określenie odkształceń poszczególnych warstw przekroju;
- obliczenie siły normalnej w betonie i momentu zginającego tej siły
względem początku układu współrzędnych;
- obliczenie przekroju zbrojenia As1 i As2 z równań równowagi sił w przekroju i obciążenia zewnętrznego: nN=0 oraz nM=0
- jeśli As1 i As2> -0,05 cm2 (z uwagi na określoną dokładność obliczeń) obliczenie n As, jeśli As1 lub
As2O-0,05 cm2
przejście do pkt. 6,
- powrót do punktu 2 i zmiana krzywizny przekroju, lub, jeśli sprawdzono cały zakres krzywizny dla założonego odkształcenia skrajnego ściskanego włókna przekroju, powrót do punktu 1 i zmiana tego odkształcenia.
- jako wynik zapamiętane jest to zbrojenie As1 i As2, dla którego n As osiąga minimum.
Wyniki
W wyniku przeprowadzanych obliczeń program informuje nas o nośności elementu lub wymaganym zbrojeniu - w zależności od wybranego trybu obliczeń (sprawdzanie nośności lub wymiarowanie).
Wyniki podzielone są na następujące działy: Parametry ogólne, Dane geometryczne,
Obciążenia, Obliczenia, Siły wewnętrzne bez uwzględnienia wpływu smukłości,
Siły wewnętrzne z uwzględnieniem wpływu smukłości, Wyniki obliczeń.
Raporty z obliczeń
Po wywołaniu funkcji obliczenia na ekranie pojawia się okno Konfiguracja raportu, w którym możemy zdecydować jakie dane i wyniki ma zawierać raport.
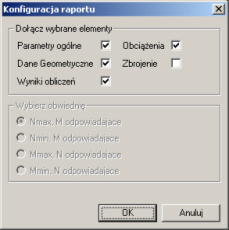
Pole Wybierz obwiednię jest aktywne tylko w przypadku współpracy z programem Rama 2D. Po przekazaniu danych i wyników obliczeń statycznych z programu Rama 2D do programu Słup żelbetowy, a następnie uruchomieniu obliczeń na ekranie pojawi się okno Konfiguracja raportu, gdzie dodatkowo możemy zdecydować, dla której z obwiedni zostaną przeprowadzone obliczenia. Funkcja wyboru obwiedni dotyczy wyłącznie trybu Wymiarowanie.
|
 Ukryj
Ukryj
