Najczęstsze przypadki błędów popełnianych przez użytkowników przy modelowaniu układu sprowadzają się do dwóch bardzo istotnych kwestii, mających bardzo poważne skutki w obliczeniach statycznych.
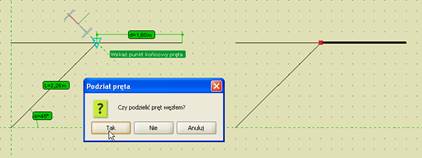
Pierwsza z nich dotyczy wprowadzania prętów do układu i polega na przeświadczeniu, że dwa stykające się ze sobą na ekranie monitora pręty są ze sobą zawsze połączone. Aby tak było, wszystkie pręty stykające się w danym węźle muszą tam mieć swój koniec lub początek, czyli muszą się w tym węźle kończyć lub zaczynać. Niestety, często zdarza się, że początkujący użytkownik dociąga wprowadzany pręt do punktu leżącego na długości innego, istniejącego pręta i nie tworzy w tym miejscu na pręcie węzła (opcja podziału pręta węzłem). W takim przypadku pręty te stykają się ze sobą, ale w modelu statycznym nie są między sobą połączone. W konsekwencji użytkownik uzyskuje często układy geometrycznie zmienne (luźne pręty) lub wyniki obliczeń statycznych są całkowicie niezgodne z jego oczekiwaniem. Analogiczna sytuacja występuje w przypadku widocznego na ekranie przecięcia dwóch elementów. Jeśli jeden z prętów w punkcie przecięcia nie ma swojego węzła początkowego lub końcowego, to nie jest on połączony w tym punkcie z innymi elementami.
Uwaga:
Aby połączyć wprowadzany pręt układu z innym istniejącym prętem na jego długości, należy w miejscu ich styku utworzyć węzeł (podzielić istniejący pręt węzłem).

Rys. 3.77 Wprowadzany pręt połączony w węźle
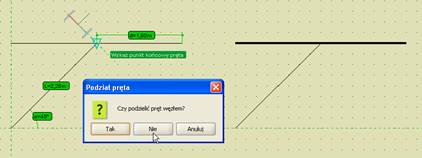
Rys. 3.78 Wprowadzany pręt niepołączony (luźny)
Drugi najczęściej spotykany problem w programie dotyczy sposobu połączenia prętów w węźle. Generalnie węzeł wypełniony czerwonym kolorem jest węzłem sztywnym, natomiast węzeł bez wypełnienia (rysowany tylko obwódką), z prętami „urwanymi” przed dojściem do węzła, jest węzłem przegubowym. W przypadku węzłów przegubowych bardzo istotna jest druga część definicji połączenia. W programie można definiować węzły, w których część prętów dochodzi do węzła przegubowo, a część jest połączona ze sobą w tym samym węźle sztywno. Wówczas przeważnie taki węzeł rysowany jest na ekranie samą obwódką bez wypełnienia. O tym czy dany pręt dochodzi do węzła przegubowo, decydują dwa warunki: musi on być przerwany przed obwódką węzła i nie może on być połączony linią z innym prętem dochodzącym do tego węzła. W każdym innym przypadku rozpatrywany pręt połączony jest sztywno z innymi prętami schodzącymi się w węźle (tymi, z którymi połączony jest linią).
|
|
|
|
Pełny węzeł sztywny
|
Pełny węzeł przegubowy |
|
|
|
|
Pręty nr 1 i 2 zesztywnione, a nr 3 i 4 przegubowe
|
Pręty nr 3 i 4 zesztywnione, a nr 1 i 2 przegubowe
|
|
|
|
|
Pręty nr 1 i 3 zesztywnione, a nr 2 i 4 przegubowe
|
Pręty nr 1, 3 i 4 zesztywnione, a nr 2 przegubowy
|
Rys. 3.79 Szczegóły połączeń w węzłach
W przypadku gdy dwa zesztywniane w węźle pręty są współliniowe lub prawie współliniowe, linia je łącząca przechodzi przez węzeł. We wszystkich pozostałych przypadkach linia łącząca pręty zesztywniane w węźle przebiega poza węzłem. W konsekwencji w skrajnym przypadku możemy otrzymać widok węzła jak niżej:
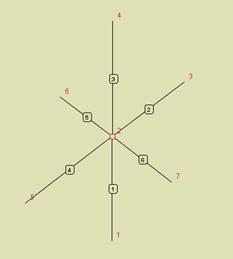
Rys. 3.80 Trzy grupy prętów zesztywnionych połączone między sobą
przegubami
Widok węzła na powyższym rysunku oznacza, że występują trzy grupy prętów zesztywnianych, między którymi występują połączenia przegubowe.
Zesztywnione są tu pręty współliniowe ujęte w nawiasy: (1 i 3); (4 i 2); (6 i 5).
Należy jeszcze zwrócić uwagę na jeden bardzo poważny problem występujący w układach liczonych przestrzennie. Dotyczy on geometrycznej niezmienności układu. Trzeba tu zawsze pamiętać, że układ, który w obliczeniach płaskich jest geometrycznie niezmienny, w obliczeniach przestrzennych w pewnych przypadkach może być geometrycznie zmienny. Rozważmy przykład najprostszej płaskiej ramy sztywnej podpartej przegubowo, jak na rysunku poniżej:
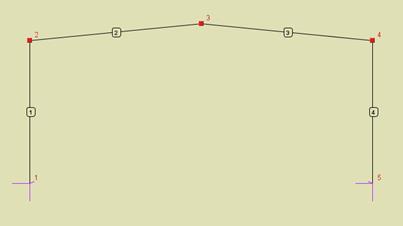
Rys. 3.81 Płaska rama sztywna podparta przegubowo
Układ taki, pod wpływem dowolnych
obciążeń działających w płaszczyźnie ramy, będzie się liczył w programie
R3D3 i wyniki obliczeń będą prawidłowe. Jednak w ogólnym przypadku
obciążenia, w Ramie 3D, jest to układ geometrycznie
zmienny. Wystarczy założyć dowolne obciążenie prostopadłe do płaszczyzny ramy i
obliczenia zostaną przerwane, a użytkownik zostanie poinformowany o
geometrycznej zmienności układu. W przypadku zadania obciążeń tylko w
płaszczyźnie ramy mamy tu do czynienia z układem samostatecznym (dlatego da się
go policzyć w programie R3D3). Aby zabezpieczyć się przed ryzykiem
wystąpienia obciążeń prostopadłych do układu, wystarczy w tym przypadku
zablokować możliwość obrotu z płaszczyzny układu w miejscach podparcia.
Oczywiście przedstawiony układ jest banalny, lecz w ogólnym przypadku złożonych
układów przestrzennych nałożenie więzi eliminujących geometryczną zmienność
układu może wcale nie być takie proste i wymaga sporego doświadczenia w zakresie
statyki. W wersji płaskiej programu - R2D2 opisane powyżej
zabezpieczenia nie są konieczne, gdyż z jednej strony nie ma możliwości
wprowadzenia obciążeń prostopadłych do płaszczyzny układu, a z drugiej program
sam w odpowiedni sposób dodaje niezbędne
i niewidoczne dla użytkownika
więzi, eliminując możliwość wystąpienia geometrycznej zmienności z płaszczyzny
układu.