Rozkład obciążenia powierzchniowego na wybrane pręty
i węzły układu

Po zdefiniowaniu obciążenia powierzchniowego wykonywany jest automatyczny rozkład całości obciążenia powierzchniowego na poszczególne węzły
i pręty przypisane do tego obciążenia. Rozkład dokonywany jest przez dyskretyzację obszaru obciążenia, gdzie głównym kryterium rozdziału jest odległość obciążenia od poszczególnych rzutów prętów na płaszczyznę obciążenia i ich węzłów. Obciążenie, które jest jednocześnie równo odległe od kilku prętów (węzłów), rozdzielane jest proporcjonalnie na wszystkie te pręty (węzły). Ponieważ obszar obciążenia podlega dyskretyzacji, rozkład obciążenia dokonywany jest z określoną dokładnością, zależną głównie od zastosowanej gęstości podziału. Tak wyznaczone obciążenia (w postaci dyskretnych sił skupionych), zrzutowane zostaną prostopadle na pręt i przypisywane są do poszczególnych prętów i ich węzłów, a następnie, w przypadku węzłów, sumowane do sił skupionych, zaś dla prętów zamieniane na odpowiednie obciążenie ciągłe, którego położenie i wartość wypadkowej pokrywa się z wypadkową wyjściowych sił skupionych (zachowana jest równowaga sił i momentów względem węzłów końcowych pręta). Metoda ta zapewnia z jednej strony wystarczającą dokładność do celów inżynierskich (zachowane są wartości reakcji na węzły,
a różnice w momentach, w ekstremalnym punkcie na długości danego pręta,
w żadnym wypadku nie powinny przekraczać ok. 25%). Z drugiej generuje minimalną ilość obciążeń (maksymalnie 2 siły skupione w węzłach i liniowe obciążenie ciągłe rozłożone na całej długości pręta). W trakcie wykonywania rozkładu obciążenia powierzchniowego na poszczególne pręty i węzły, rozkładana jest zawsze cała zadana powierzchnia obciążenia. Tak więc suma wszystkich sił węzłowych i obciążeń ciągłych przypisanych do danego obciążenia powierzchniowego odpowiada wartości wypadkowej tego obciążenia. Ponieważ jednak zastosowana metoda jest dyskretna, ma ona swoją dokładność określoną współczynnikiem sprawności rozkładu, który definiowany jest
w programie jako stosunek sumy wszystkich obciążeń przyłożonych do prętów i węzłów po rozkładzie do całkowitej wypadkowej założonego obciążenia powierzchniowego. Czym współczynnik sprawności jest bliższy wartości 1.0, tym globalna dokładność rozkładu jest większa. Na dokładność rozkładu  (poza stopniem dyskretyzacji) ma również wpływ odległość między poszczególnymi wybranymi prętami; im ta odległość większa, tym rozkład dokładniejszy. Dokładność rozkładu obciążeń na poszczególne pręty można również zwiększyć, dzieląc te pręty węzłami na odcinki, przy czym wydłużony będzie wówczas czas rozkładu obciążenia powierzchniowego. Stopień dyskretyzacji obszaru obciążenia oraz podział prętów i odległość między prętami mają większy wpływ na rozkład na poszczególnych prętach niż na globalny rozkład całego obciążenia powierzchniowego.

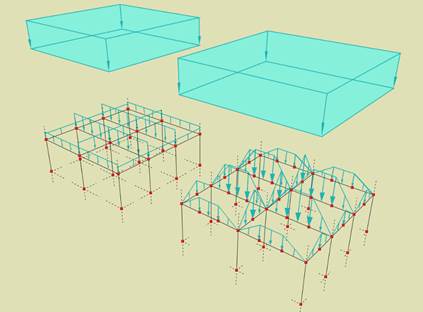
Rys. 7.38 Dwa różne rozkłady takiego samego obciążenia

 zależnie od podziału prętów

W przypadku zaznaczenia w dolnej części okna definicji obciążeń powierzchniowych przełącznika Rozkład tylko w węzłach – całość obciążenia powierzchniowego sprowadzana jest jedynie do obciążeń skupionych w wszystkich węzłach zaznaczonych prętów, z pominięciem wszelkich obciążeń ciągłych na prętach (sam podział na pola przypisane poszczególnym prętom
i węzłom nie ulega jednak w tym przypadku zmianie). Przykładowe podglądy rozkładu obciążeń na płaszczyźnie obciążenia przedstawiono poniżej:

Rys. 7.39 Przykłady podglądu rozkładu obciążenia powierzchniowego