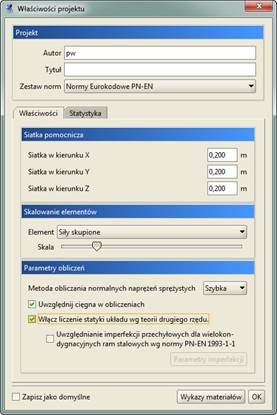
Aby wykonać obliczenia statyczne projektu wg teorii II rzędu, należy taką opcję ustawić przed obliczeniami w oknie Własności projektu (opcja Włącz liczenie statyki układu wg teorii drugiego rzędu).

Rys. 10.1 Włączanie obliczeń statycznych wg teorii II rzędu
W takim trybie obliczenia statyczne mogą być wykonane jedynie dla zdefiniowanych przez użytkownika kombinacji (suma grup z przypisanymi do nich współczynnikami) i wybranych grup obciążeń (analogicznie jak w przypadku cięgien). W przypadku obliczeń wg teorii II rzędu nie ma możliwości uzyskania wyników dla automatycznej obwiedni, budowanej przez program na podstawie zdefiniowanych grup obciążeń, przypisanych do nich parametrów, oraz zadanych relacji między grupami zmiennymi. W przypadku kombinacji należy pamiętać, że w tym przypadku, tak jak dla układów z cięgnami, również nie obowiązuje zasada superpozycji i wyniki uzyskujemy tylko od całej kombinacji, która w programie widziana jest jako „supergrupa”, będąca sumą obciążeń wszystkich grup składających się na daną kombinację, wymnożonych prze odpowiednie współczynniki.
W przypadku
obliczeń statycznych wg Eurokodu współczynniki przypisane poszczególnym grupom w
ramach kombinacji powinny być ilorazem odpowiedniego współczynnika obciążenia
dla danej grupy stałej lub zmiennej oraz odpowiedniego współczynnika
kombinacyjnego dla grup zmiennych, z uwzględnieniem jego modyfikacji dla
wybranej grupy wiodącej. W tym trybie, o wartościach przyjętych współczynników w
ramach kombinacji oraz wyborze grupy zmiennej wiodącej, decyduje zawsze
użytkownik po przez przypisanie odpowiednich ilorazów współczynników
poszczególnym grupom obciążeń, w ramach zdefiniowanych w projekcie kombinacji.
Wynika to stąd, że dla obliczeń według teorii II rzędu (analogicznie jest
również dla układów z cięgnami) nie mogą być dostępne wyniki sił wewnętrznych i
przemieszczeń od poszczególnych grup składających się na daną kombinację,
a
jedynie wyniki dla całej kombinacji. Z tego też powodu przy obliczeniach wg norm
PN lub Eurokodu, przy obliczeniach prowadzonych wg teorii II rzędu lub dla
układów z cięgnami, osobne kombinacje powinny być zdefiniowane dla stanu
granicznego nośności, a osobne dla stanu granicznego użytkowania (inne
współczynniki). W tych też przypadkach wszystkie współczynniki powinny być
przypisane do grup w kombinacji (po stronie obciążeń), gdyż po stronie wyników
nie ma możliwości wydzielenia wartości od poszczególnych grup w kombinacji i
pomnożenia ich przez odpowiednie współczynniki.
Przy
obliczeniach wg teorii II rzędu nie są wyliczane wyniki dla grupy typu „multi”
oraz grup ruchomych. Grupy te nie biorą również udziału
w budowie kombinacji
użytkownika. Aby uwzględnić w wynikach kombinacji udział takich grup, należy
przed zbudowaniem kombinacji rozbić te grupy na zwykłe grupy zmienne i wybrać
jedną z nich w przypadku obciążenia ruchomego lub kilka w przypadku grup
zmiennych powstałych po rozbiciu grupy „multi”.
W trakcie wykonywania obliczeń projektu wg teorii II rzędu w pewnych sytuacjach mogą zostać one przerwane jednym z następujących komunikatów:
1.
Obliczenia wg teorii drugiego rzędu nie uzyskały ustalonej zbieżności
procesu iteracyjnego. Prawdopodobnie niedostateczna sztywność układu. –
komunikat występuje, gdy przekroczona zostanie setna iteracja
w procesie
obliczeń według teorii II rzędu lub rozwiązywanie układu równań zakończy się
niepowodzeniem ze względu na rozbieżność iteracji w procesie rozwiązania układu
równań.
2.
Model zbyt wiotki dla zadanego schematu obciążeń. Obliczenia
przerwane. – komunikat występuje, gdy znaczące przemieszczenia dowolnego
węzła o wartości powyżej 1 mm, uzyskane z obliczeń w teorii I rzędu,
w danej
iteracji obliczeń według teorii II rzędu przekroczą 5-krotność jego
przemieszczeń z teorii pierwszego rzędu lub przekroczyły 2.5% największej
rozpiętości modelu w kierunku x lub z. Pierwszy napotkany węzeł, dla którego
spełniony jest jeden z powyżej opisanych warunków, pozostanie wyselekcjonowany
po zamknięciu komunikatu.
3. Model zawiera pręty o smukłości większej niż 350 lub siła normalna jest większa niż 90% siły krytycznej w tych prętach. Do obliczeń według teorii drugiego rzędu powinny być one przyjęte jako cięgna. Obliczenia przerwane. – sprawdzenie wykonywane dla wszystkich prętów układu niebędących cięgnami po wykonaniu obliczeń wg teorii pierwszego rzędu wewnątrz obliczeń według teorii II rzędu. Pręty, dla których spełniony jest jeden z powyżej opisanych warunków, pozostaną wyselekcjonowane po zamknięciu komunikatu.
W
zasadzie wszystkie trzy powyższe komunikaty informują użytkownika
o zbyt
małej sztywności prętów liczonego układu, przy czym w przypadku wystąpienia
trzeciego komunikatu lepszym wyjściem niż zwiększanie sztywności jest zamiana
wskazanych przez program prętów na pręty typu cięgno.
Obliczenia według teorii II rzędu oparte są na równaniu różniczkowym zginania pręta z udziałem siły osiowej. Równania równowagi są zapisane dla układu zdeformowanego (nie obowiązuje zasada zesztywnienia). Poszczególne współczynniki macierzy sztywności zależą od wartości siły normalnej działającej w elemencie.
Obliczenia numeryczne są przeprowadzone w sposób iteracyjny. Na każdym kroku iteracji jest aktualizowana wartość współczynników macierzy sztywności dla aktualnej geometrii układu i wartości sił normalnych. Generalnie w metodzie tej nie obowiązuje zasada superpozycji, stąd obliczenia są przeprowadzane dla sumy wszystkich grup obciążeń występujących w danej kombinacji lub dla pojedynczej grupy obciążeń. Stąd dla obliczeń wg teorii II rzędu nie działa w programie opcja automatycznej obwiedni.
W przypadku prętów zbyt smukłych iteracja może być rozbieżna, dlatego w przypadku występowania prętów ściskanych o smukłości większej niż 350 pojawia się komunikat o konieczności zadeklarowania takiego pręta jako cięgno.
W przeciwieństwie do teorii I rzędu może się zdarzyć, że przemieszczenia będą przyrastały do bardzo dużych wartości, a w przypadku skrajnym będą dążyć do nieskończoności. Program sygnalizuje to komunikatem, że iteracja jest rozbieżna i układ jest geometrycznie zmienny dla teorii II rzędu. Przykładowo dla poniższego zadania:
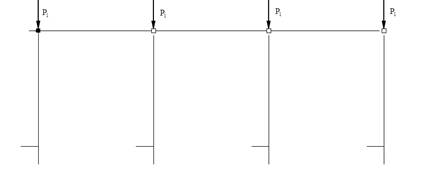
Rys. 10.2 Przykład
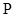
w teorii I rzędu otrzymujemy zawsze rozwiązania niezależnie od wartości sił P1. W obliczeniach dla teorii II rzędu wraz ze wzrostem wartości sił P1 rosną deformacje, aż przy pewnych wartościach sił P1 (zależnych od sztywności układu) deformacje te będą tak duże, że iteracja będzie rozbieżna i otrzymamy komunikat „układ zbyt wiotki, geometrycznie zmienny”.
Przystępując do obliczeń wg teorii II rzędu trzeba pamiętać, że związki pomiędzy siłami wewnętrznymi i obciążeniami są opisane funkcjami trygonometrycznymi (dla sił ściskających) lub hiperbolicznymi (dla sił rozciągających). Użytkownik programu musi sam stworzyć poszczególne kombinacje obciążeń, włączając do nich odpowiednie grupy obciążeń wraz z przynależnymi współczynnikami przeciążenia. W wyniku obliczeń otrzymujemy deformację układu i wykresy sił wewnętrznych i naprężeń. W omawianym programie jako siły tnące przedstawiono wykresy sił poprzecznych prostopadłych do niezdeformowanej osi pręta, a nie rzeczywiste siły tnące, które są prostopadłe do zdeformowanej osi pręta.